A) FACTORIAL.- La factorial está relacionada con el cálculo del número de maneras en las que un conjunto de cosas puede arreglarse en orden.
El número de maneras en el que las n cosas pueden arreglarse en orden es:
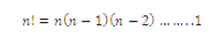
Donde n! se llama el factorial de n y 0! se define como 1
B) PERMUTACIONES.-En muchos casos se necesita saber el número de formas en las que un subconjunto de un grupo completo de cosas puede arreglarse en orden. Cada posible arreglo es llamado permutación. Si un orden es suficiente para construir otro subconjunto, entonces se trata de permutaciones.
El número de maneras para arreglar r objetos seleccionados a la vez de n objetos en orden, es decir, el número de permutaciones de n elementos tomados r a la vez es:
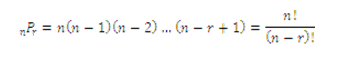
C) COMBINACIONES
En muchos situaciones no interesa el orden de los resultados, sino sólo el número de maneras en las que r objetos pueden seleccionarse a partir de n cosas, sin consideración de orden. Si dos subconjntos se consideran iguales debido a que simplemente se han reordenado los mismos elementos, entonces se trata de combinaciones.
El número de maneras para arreglar r objetos seleccionados a la vez de n objetos, sin considerar el orden, es decir, el número de combinaciones de n elementos tomados r a la vez es:
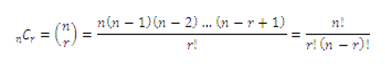
Conceptos básicos
A) EXPERIMENTO.- Es toda acción sobre la cual vamos a realizar una medición u observación, es decir cualquier proceso que genera un resultado definido.
B) EXPERIMENTO ALEATORIO.- Es toda actividad cuyos resultados no se determinan con certeza. Ejemplo: lanzar una moneda al aire. No podemos determinar con toda certeza ¿cuál será el resultado al lanzar una moneda al aire?, por lo tanto constituye un experimento aleatorio.
C) ESPACIO MUESTRAL (S).- Es un conjunto de todos los resultados posibles que se pueden obtener al realizar un experimento aleatorio. Ejemplo: sea el experimento E: lanzar un dado y el espacio muestral correspondiente a este experimento es: S = (1, 2, 3, 4, 5, 6(.
D) PUNTO MUESTRAL.- Es un elemento del espacio muestral de cualquier experimento dado.
E) EVENTO O SUCESO.- Es todo subconjunto de un espacio muestral. Se denotan con letras mayúsculas: A, B, etc. Los resultados que forman parte de este evento generalmente se conocen como "resultados favorables". Cada vez que se observa un resultado favorable, se dice que "ocurrió" un evento. Ejemplo: Sea el experimento E: lanzar un dado. Un posible evento podría ser que salga número par. Definimos el evento de la siguiente manera: A = sale número par = (2, 4, 6(, resultados favorables n(E) = 3
Los eventos pueden ser:
i) Evento cierto.- Un evento es cierto o seguro si se realiza siempre. Ejemplo: Al introducirnos en el mar, en condiciones normales, es seguro que nos mojaremos.
ii) Evento imposible.- Un evento es imposible si nunca se realiza. Al lanzar un dado una sola vez, es imposible que salga un 10
iii) Evento probable o aleatorio.- Un evento es aleatorio si no se puede precisar de antemano el resultado. Ejemplo: ¿Al lanzar un dado, saldrá el número 3?
F) PROBABILIDAD.- Es el conjunto de posibilidades de que un evento ocurra o no en un momento y tiempo determinado. Dichos eventos pueden ser medibles a través de una escala de 0 a 1, donde el evento que no pueda ocurrir tiene una probabilidad de 0 (evento imposible) y un evento que ocurra con certeza es de 1 (evento cierto).
La probabilidad de que ocurra un evento, siendo ésta una medida de la posibilidad de que un suceso ocurra favorablemente, se determina principalmente de dos formas: empíricamente (de manera experimental) o teóricamente (de forma matemática).
i) Probabilidad empírica.- Si E es un evento que puede ocurrir cuando se realiza un experimento, entonces la probabilidad empírica del evento E, que a veces se le denomina definición de frecuencia relativa de la probabilidad, está dada por la siguiente fórmula:
Nota: P(E), se lee probabilidad del evento E
ii) Probabilidad teórica.- Si todos los resultados en un espacio muestral S finito son igualmente probables, y E es un evento en ese espacio muestral, entonces la probabilidad teórica del evento E está dada por la siguiente fórmula, que a veces se le denomina la definición clásica de la probabilidad, expuesta por Pierre Laplace en su famosa Teoría analítica de la probabilidad publicada en 1812:
G) POSIBILIDADES.- Las posibilidades comparan el número de resultados favorables con el número de resultados desfavorables. Si todos los resultados de un espacio muestral son igualmente probables, y un número n de ellos son favorables al evento E, y los restantes m son desfavorables a E, entonces las posibilidades a favor de E sonde de n(E) a m(E), y lasposibilidades en contra de E son de m(E) a n(E)
Ejemplos ilustrativos: Mathías se le prometió comprar 6 libros, tres de los cuales son de Matemática. Si tiene las mismas oportunidades de obtener cualquiera de los 6 libros, determinar las posibilidades de que le compren uno de Matemática.
Solución:
Número de resultados favorables = n(E) = 3
Número de resultados desfavorables = m(E) = 3
Posibilidades a favor son n(E) a m(E), entonces,
Posibilidades a favor = 3 a 3, y simplificando 1 a 1.
Nota: A las posibilidades de 1 a 1 se les conoce como "igualdad de posibilidades" o "posibilidades de 50-50"
Reglas de la probabilidad
A) REGLA DE LA ADICIÓN DE PROBABILIDADES
i) REGLA GENERAL PARA EVENTOS NO MUTUAMENTE EXCLUYENTES
Si A y B son dos eventos no mutuamente excluyentes (eventos intersecantes), es decir, de modo que ocurra A o bien B o ambos a la vez (al mismo tiempo), entonces se aplica la siguiente regla para calcular dicha probabilidad:
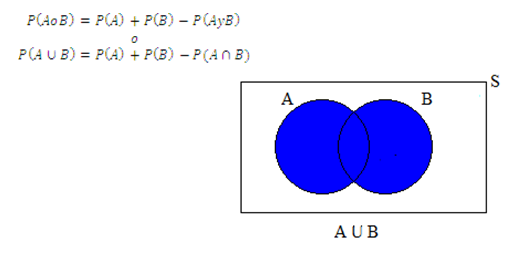
En donde:
El conectivo lógico "o" corresponde a la "unión" en la teoría de conjuntos (o =)
El conectivo "y" corresponde a la "intersección" en la teoría de conjuntos (y =)
El espacio muestral (S) corresponde al conjunto universo en la teoría de conjuntos
ii) REGLA PARTICULAR O ESPECIAL PARA EVENTOS MUTUAMENTE EXCLUYENTES
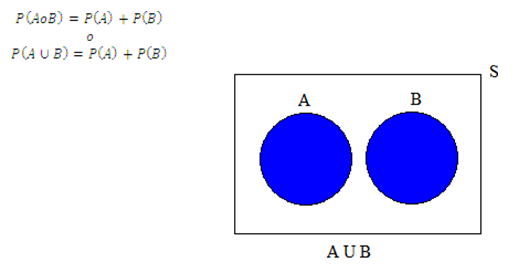
En donde:
El conectivo lógico "o" corresponde a la "unión" en la teoría de conjuntos (o =)
El espacio muestral (S) corresponde al conjunto universo en la teoría de conjuntos
B) REGLA DE LA MULTIPLICACIÓN DE PROBABILIDADES
i) REGLA GENERAL PARA EVENTOS DEPENDIENTES
Si A y B son dos eventos dependientes, es decir, si la ocurrencia de A afecta la probabilidad de ocurrencia de B, entonces, dicha probabilidad de calcula empleando la siguiente regla:
Nota:
La probabilidad del evento B, calculada bajo la suposición de que el evento A ha ocurrido, se denomina probabilidad condicional de B, dado A, y se denota por P (B/A).
ii) REGLA PARTICULAR O ESPECIAL PARA EVENTOS INDEPENDIENTES
Si A y B son dos eventos independientes, es decir, si el conocimiento de la incidencia de uno de ellos no tiene efecto en la probabilidad de ocurrencia del otro, entonces, para calcular la probabilidad de dichos eventos se aplica la siguiente regla:
1.4) PROBABILIDAD TOTAL Y TEOREMA DE BAYES
A) PROBABILIDAD TOTAL
B) TEOREMA DE BAYES
El teorema de Bayes se utiliza para revisar probabilidades previamente calculadas cuando se posee nueva información. Desarrollado por el reverendo Thomas Bayes en el siglo XVII, el teorema de Bayes es una extensión de lo que ha aprendido hasta ahora acerca de la probabilidad condicional.
Comúnmente se inicia un análisis de probabilidades con una asignación inicial, probabilidad a priori. Cuando se tiene alguna información adicional se procede a calcular las probabilidades revisadas o a posteriori. El teorema de Bayes permite calcular las probabilidades a posteriori y es:
- DISTRIBUCIONES DISCRETAS
A) INTRODUCCIÓN
Una distribución de probabilidad es una representación de todos los resultados posibles de algún experimento y de la probabilidad relacionada con cada uno.
Una distribución de probabilidad es discreta cuando los resultados posibles del experimento son obtenidos de variables aleatorias discretas, es decir, de variables que sólo puede tomar ciertos valores, con frecuencia números enteros, y que resultan principalmente del proceso de conteo.
Ejemplos de variables aleatorias discretas son:
Número de caras al lanzar una moneda
El resultado del lanzamiento de un dado
Número de hijos de una familia
Número de estudiantes de una universidad
Ejemplo ilustrativo
Sea el experimento aleatorio de lanzar 2 monedas al aire. Determinar la distribución de probabilidades del número de caras.
Solución:
El espacio muestral es S = {CC, CS, SC, SS}
La probabilidad de cada punto muestral es de 1/4, es decir, P(CC) = P(CS) = P(SC) = P(SS) = 1/4
La distribución de probabilidades del número de caras se presenta en la siguiente tabla:
Resultados (N° de Caras)
|
Probabilidad
|
0
|
1/4 = 0,25 = 25%
|
1
|
2/4 = 0,50 = 50%
|
2
|
1/4 = 0,25 = 25%
|
El gráfico de distribuciones de probabilidad en 3D elaborado en Excel se muestra en la siguiente figura:
Interpretación:
La probabilidad de obtener 0 caras al lanzar 2 monedas al aire es de 1/4 = 0,25 = 25%
La probabilidad de obtener una cara al lanzar 2 monedas al aire es de 2/4 = 0,5 = 50%
La probabilidad de obtener 2 caras al lanzar 2 monedas al aire es de 1/4 = 0,25 = 25%
B) LA MEDIA Y LA VARIANZA DE LAS DISTRIBUCIONES DISCRETAS
i) Media
La media llamada también valor esperado, esperanza matemática o simplemente esperanza de una distribución de probabilidad discreta es la media aritmética ponderada de todos los resultados posibles en los cuales los pesos son las probabilidades respectivas de tales resultados. Se halla multiplicando cada resultado posible por su probabilidad y sumando los resultados. Se expresa mediante la siguiente fórmula:
ii) Varianza
La varianza es el promedio de las desviaciones al cuadrado con respecto a la media. La varianza mide la dispersión de los resultados alrededor de la media y se halla calculando las diferencias entre cada uno de los resultados y su media, luego tales diferencias se elevan al cuadrado y se multiplican por sus respectivas probabilidades, y finalmente se suman los resultados. Se expresa mediante la siguiente fórmula:
Ejemplo ilustrativo:
Hallar la esperanza matemática, la varianza y la desviación estándar del número de caras al lanzar tres monedas al aire.
Solución:
El espacio muestral es S = {CCC, CCS, CSC, SCC, CSS, SCS, SSC, SSS}
La probabilidad de cada punto muestral es de 1/8
Se elabora las distribuciones de probabilidad y se realiza los cálculos respectivos. Estos resultados se presentan en la siguiente tabla:
Interpretación:
C) DISTRIBUCIÓN BINOMIAL
i) Definición:
Cuando se dispone de una expresión matemática, es factible calcular la probabilidad de ocurrencia exacta correspondiente a cualquier resultado específico para la variable aleatoria.
La distribución de probabilidad binomial es uno de los modelos matemáticos (expresión matemática para representar una variable) que se utiliza cuando la variable aleatoria discreta es el número de éxitos en una muestra compuesta por n observaciones.
ii) Propiedades:
- La muestra se compone de un número fijo de observaciones n
- Cada observación se clasifica en una de dos categorías, mutuamente excluyentes (los eventos no pueden ocurrir de manera simultánea. Ejemplo: Una persona no puede ser de ambos sexos) y colectivamente exhaustivos (uno de los eventos debe ocurrir. Ejemplo: Al lanzar una moneda, si no ocurre cruz, entonces ocurre cara). A estas categorías se las denominaéxito y fracaso.
- La probabilidad de que una observación se clasifique como éxito, p, es constante de una observación o otra. De la misma forma, la probabilidad de que una observación se clasifique como fracaso, 1-p, es constante en todas las observaciones.
- La variable aleatoria binomial tiene un rango de 0 a n
iii) Ecuación:
iv) Media de la distribución binomial
v) Desviación estándar de la distribución binomial
D) DISTRIBUCIÓN DE POISSON
i) Introducción.- Muchos estudios se basan en el conteo de las veces que se presenta un evento dentro de un área de oportunidad dada. El área de oportunidad es una unidad continua o intervalo de tiempo o espacio (volumen o área) en donde se puede presentar más de un evento. Algunos ejemplos serían los defectos en la superficie de un refrigerador, el número fallas de la red en un día, o el número de pulgas que tiene un perro. Cuando se tiene un área de oportunidad como éstas, se utiliza la distribución de Poisson para calcular las probabilidades si:
- Le interesa contar las veces que se presenta un evento en particular dentro de un área de oportunidad determinada. El área de oportunidad se define por tiempo, extensión, área, volumen, etc.
- La probabilidad de que un evento se presente en un área de oportunidad dada es igual para todas las áreas de oportunidad.
- El número de eventos que ocurren en un área de oportunidad es independiente del número de eventos que se presentan en cualquier otra área de oportunidad.
- La probabilidad de que dos o más eventos se presenten en un área de oportunidad tiende a cero conforme esa área se vuelve menor.
ii) Fórmula.-
E) DISTRIBUCIÓN HIPERGEOMÉTRICA
i) Definición
La distribución binomial es apropiada sólo si la probabilidad de un éxito permanece constante. Esto ocurre si el muestreo se realiza con reemplazo en una población grande. Sin embrago, si la población es pequeña y ocurre sin reemplazo, la probabilidad de éxito variará, y la distribución hipergeométrica es que se utiliza.
ii) Fórmula
Se calcula empleando la siguiente fórmula:
Donde:
C = combinación
N = tamaño de la población
r = número de éxitos en la población
n = tamaño de la muestra
X = número de éxitos en la muestra
Notas:
- Si se selecciona una muestra sin reemplazo de una población grande conocida y contiene una proporción relativamente grande de la población, de manera que la probabilidad de éxito varía de una selección a la siguiente, debe utilizarse la distribución hipergeométrica.
- Cuando tamaño de la población (N) es muy grande, la distribución hipergeométrica tiende aproximarse a la binomial.
Ejemplo ilustrativo
Si se extraen juntas al azar 3 bolas de una urna que contiene 6 bolas rojas y 4 blancas. ¿Cuál es la probabilidad de que sean extraídas 2 bolas rojas?.
Solución:
Los datos son: N =10; r = 6; n = 3 y X= 2
Aplicando la fórmula se obtiene:
2.2 DISTRIBUCIONES CONTINUAS
A) INTRODUCCIÓN
Una distribución de probabilidad es continua cuando los resultados posibles del experimento son obtenidos de variables aleatorias continuas, es decir, de variables cuantitativas que pueden tomar cualquier valor, y que resultan principalmente del proceso de medición.
Ejemplos de variables aleatorias continuas son:
La estatura de un grupo de personas
El tiempo dedicado a estudiar
La temperatura en una ciudad
B) DISTRIBUCIÓN EXPONENCIAL
i) Definición
La distribución de Poisson calcula el número de eventos sobre alguna área de oportunidad (intervalo de tiempo o espacio), la distribución exponencial mide el paso del tiempo entre tales eventos. Si el número de eventos tiene una distribución de Poisson, el lapso entre los eventos estará distribuido exponencialmente.
ii) Fórmula
La probabilidad de que el lapso de tiempo sea menor que o igual a cierta cantidad x es:
C) DISTRIBUCIÓN UNIFORME
i) Definición
Es una distribución en el intervalo 
en la cual las probabilidades son las mismas para todos los posibles resultados, desde el mínimo de a hasta el máximo de b. El experimento de lanzar un dado es un ejemplo que cumple la distribución uniforme, ya que todos los 6 resultados posibles tienen 1/6 de probabilidad de ocurrencia.
en la cual las probabilidades son las mismas para todos los posibles resultados, desde el mínimo de a hasta el máximo de b. El experimento de lanzar un dado es un ejemplo que cumple la distribución uniforme, ya que todos los 6 resultados posibles tienen 1/6 de probabilidad de ocurrencia.
ii) Función de densidad de una distribución uniforme (altura de cada rectángulo en la gráfica anterior) es:
Donde:
a = mínimo valor de la distribución
b = máximo valor de la distribución
b – a = Rango de la distribución
iii) La media, valor medio esperado o esperanza matemática de una distribución uniforme se calcula empleando la siguiente fórmula:
iv) La varianza de una distribución uniforme se calcula empleando la siguiente fórmula:
v) La probabilidad de que una observación caiga entre dos valores se calcula de la siguiente manera:
D) DISTRIBUCIÓN NORMAL
i) Reseña histórica
Abrahan De Moivre (1733) fue el primero en obtener la ecuación matemática de la curva normal. Kart Friedrich Gauss y Márquez De Laplece (principios del siglo diecinueve) desarrollaron más ampliamente los conceptos de la curva. La curva normal también es llamada curva de error, curva de campana, curva de Gauss, distribución gaussiana o curva de De Moivre.
Su altura máxima se encuentra en la media aritmética, es decir su ordenada máxima corresponde a una abscisa igual a la media aritmética. La asimetría de la curva normal es nula y por su grado de apuntamiento o curtosis se clasifica en mesocúrtica.
ii) Ecuación
Su ecuación matemática de la función de densidad es:
Nota: No existe una única distribución normal, sino una familia de distribuciones con una forma común, diferenciadas por los valores de su media y su varianza. De entre todas ellas, la más utilizada es la distribución normal estándar, que corresponde a una distribución con una media aritmética de 0 y una desviación típica de 1.
Estimación de intervalos de confianza
La estadística inferencial es el proceso de uso de los resultados derivados de las muestras para obtener conclusiones acerca de las características de una población. La estadística inferencial nos permite estimar características desconocidas como la media de la población o la proporción de la población. Existen dos tipos de estimaciones usadas para estimar los parámetros de la población: la estimación puntual y la estimación de intervalo. Una estimación puntual es el valor de un estadístico de muestra. Una estimación del intervalo de confianza es un rango de números, llamado intervalo, construido alrededor de la estimación puntual. El intervalo de confianza se construye de manera que la probabilidad del parámetro de la población se localice en algún lugar dentro del intervalo conocido.
Suponga que quiere estimar la media de todos los alumnos en su universidad. La media para todos los alumnos es una media desconocida de la población, simbolizada como 
Usted selecciona una muestra de alumnos, y encuentra que la media es de 5,8. La muestra de la media 
es la estimación puntual de la media poblacional ¿Qué tan preciso es el 5,8? Para responder esta pregunta debe construir una estimación del intervalo de confianza.
Usted selecciona una muestra de alumnos, y encuentra que la media es de 5,8. La muestra de la media es la estimación puntual de la media poblacional ¿Qué tan preciso es el 5,8? Para responder esta pregunta debe construir una estimación del intervalo de confianza.
3.1) ESTIMACIÓN DEL INTERVALO DE CONFIANZA PARA LA MEDIA
Donde:
Z = valor crítico de la distribución normal estandarizada
Se llama valor crítico al valor de Z necesario para construir un intervalo de confianza para la distribución. El 95% de confianza corresponde a un valor ( de 0,05. El valor crítico Z correspondiente al área acumulativa de 0,975 es 1,96 porque hay 0,025 en la cola superior de la distribución y el área acumulativa menor a Z = 1,96 es 0,975.
Un nivel de confianza del 95% lleva a un valor Z de 1,96. El 99% de confianza corresponde a un valor ( de 0,01. El valor de Z es aproximadamente 2,58 porque el área de la cola alta es 0,005 y el área acumulativa menor a Z = 2,58 es 0,995.
3.2) ESTIMACIÓN DE INTERVALO DE CONFIANZA PARA LA MEDIA
La distribución t supone que la población está distribuida normalmente. Esta suposición es particularmente importante para n ( 30. Pero cuando la población es finita y el tamaño de la muestra constituye más del 5% de la población, se debe usar el factor finito de corrección para modificar las desviaciones estándar. Por lo tanto si cumple:
Siendo N el tamaño de la población y n el tamaño de la muestra
Antes de seguir continuando es necesario estudiar la distribución t de Student, por lo que a continuación se presenta una breve explicación de esta distribución.
Al comenzar el siglo XX, un especialista en Estadística de la Guinness Breweries en Irlanda llamado William S. Gosset deseaba hacer inferencias acerca de la media cuando la 
fuera desconocida. Como a los empleados de Guinness no se les permitía publicar el trabajo de investigación bajo sus propios nombres, Gosset adoptó el seudónimo de "Student". La distribución que desarrolló se conoce como la distribución t de Student.
fuera desconocida. Como a los empleados de Guinness no se les permitía publicar el trabajo de investigación bajo sus propios nombres, Gosset adoptó el seudónimo de "Student". La distribución que desarrolló se conoce como la distribución t de Student.
Si la variable aleatoria X se distribuye normalmente, entonces el siguiente estadístico tiene una distribución t con n - 1 grados de libertad.
Entre las principales propiedades de la distribución t se tiene:
En apariencia, la distribución t es muy similar a la distribución normal estandarizada. Ambas distribuciones tienen forma de campana. Sin embargo, la distribución t tiene mayor área en los extremos y menor en el centro, a diferencia de la distribución normal.
Como se estableció anteriormente, la distribución t supone que la variable aleatoria X se distribuye normalmente. En la práctica, sin embargo, mientras el tamaño de la muestra sea lo suficientemente grande y la población no sea muy sesgada, la distribución t servirá para estimar la media poblacional cuando sea desconocida.
Los grados de libertad de esta distribución se calculan con la siguiente fórmula
Donde n = tamaño de la muestra
3.3) ESTIMACIÓN DEL INTERVALO DE CONFIANZA PARA UNA PROPORCIÓN
Sirve para calcular la estimación de la proporción de elementos en una población que tiene ciertas características de interés.
3.4) DETERMINACIÓN DEL TAMAÑO DE LA MUESTRA
En cada ejemplo de la estimación del intervalo de confianza, usted seleccionó un tamaño de muestra sin considerar la amplitud del intervalo de confianza. En el mundo de los negocios, determinar el tamaño adecuado de la muestra es un procedimiento complicado, ya que está sujeto a las restricciones de presupuesto, tiempo y cantidad aceptada de error de muestreo. Si por ejemplo usted desea estimar la media de la cantidad de ventas en dólares de la facturas de ventas o la proporción de facturas de ventas que contienen errores, debe determinar por anticipado cuán grande sería el error de muestreo para estimar cada uno de los parámetros. También debe determinar por anticipado el nivel del intervalo de confianza a usar al estimar el parámetro poblacional.
Recordemos los siguientes conceptos básicos
Población.- Llamado también universo o colectivo, es el conjunto de todos los elementos que tienen una característica común. Una población puede ser finita o infinita. Es población finita cuando está delimitada y conocemos el número que la integran, así por ejemplo: Estudiantes de la Universidad UTN. Es población infinita cuando a pesar de estar delimitada en el espacio, no se conoce el número de elementos que la integran, así por ejemplo: Todos los profesionales universitarios que están ejerciendo su carrera.
Muestra.- La muestra es un subconjunto de la población. Ejemplo: Estudiantes de 2do Semestre de la Universidad UTN.
Sus principales características son:
Representativa.- Se refiere a que todos y cada uno de los elementos de la población tengan la misma oportunidad de ser tomados en cuenta para formar dicha muestra.
Adecuada y válida.- Se refiere a que la muestra debe ser obtenida de tal manera que permita establecer un mínimo de error posible respecto de la población.
Para que una muestra sea fiable, es necesario que su tamaño sea obtenido mediante procesos matemáticos que eliminen la incidencia del error.
Elemento o individuo.- Unidad mínima que compone una población. El elemento puede ser una entidad simple (una persona) o una entidad compleja (una familia), y se denomina unidad investigativa.
A) DETERMINACIÓN DEL TAMAÑO DE LA MUESTRA PARA LA MEDIA
Para desarrollar una fórmula que permita determinar el tamaño apropiado de la muestra para construir una estimación del intervalo de confianza para la media, recuerde la ecuación
En algunas ocasiones es posible estimar la desviación estándar a partir de datos pasados. En otras situaciones, puede hacer una cuidadosa conjetura tomando en cuenta el rango y la distribución de la variable.
De esta fórmula del error de la estimación del intervalo de confianza para la media se despeja la n, para lo cual se sigue el siguiente proceso:
Elevando al cuadrado a ambos miembros de la fórmula se obtiene:
B) DETERMINACIÓN DEL TAMAÑO DE LA MUESTRA PARA LA PROPORCIÓN
Para determinar el tamaño de la muestra necesario para estimar la proporción poblacional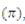 
se utiliza un método similar al método para calcular la media poblacional. Al desarrollar el tamaño de la muestra para un intervalo de confianza para la media, el error de muestreo se define por:
se utiliza un método similar al método para calcular la media poblacional. Al desarrollar el tamaño de la muestra para un intervalo de confianza para la media, el error de muestreo se define por:
Cuando en los datos se tiene el tamaño de la población se utiliza la siguiente fórmula:
Pruebas de hipótesis
En vez de estimar el valor de un parámetro, a veces se debe decidir si una afirmación relativa a un parámetro es verdadera o falsa. Es decir, probar una hipótesis relativa a un parámetro. Se realiza una prueba de hipótesis cuando se desea probar una afirmación realizada acerca de un parámetro o parámetros de una población.
Una hipótesis es un enunciado acerca del valor de un parámetro (media, proporción, etc.).
Prueba de Hipótesis es un procedimiento basado en evidencia muestral (estadístico) y en la teoría de probabilidad (distribución muestral del estadístico) para determinar si una hipótesis es razonable y no debe rechazarse, o si es irrazonable y debe ser rechazada.
La hipótesis de que el parámetro de la población es igual a un valor determinado se conoce como hipótesis nula. Una hipótesis nula es siempre una de status quo o de no diferencia. Se simboliza con el símbolo 
.Y cuando se desarrolla la prueba se asume que la hipótesis nula es verdadera y este supuesto será rechazado si se encuentran suficientesevidencias en base a la información muestral.
.Y cuando se desarrolla la prueba se asume que la hipótesis nula es verdadera y este supuesto será rechazado si se encuentran suficientesevidencias en base a la información muestral.
Siempre que se especifica una hipótesis nula, también se debe especificar una hipótesis alternativa, o una que debe ser verdadera si se encuentra que la hipótesis nula es falsa.
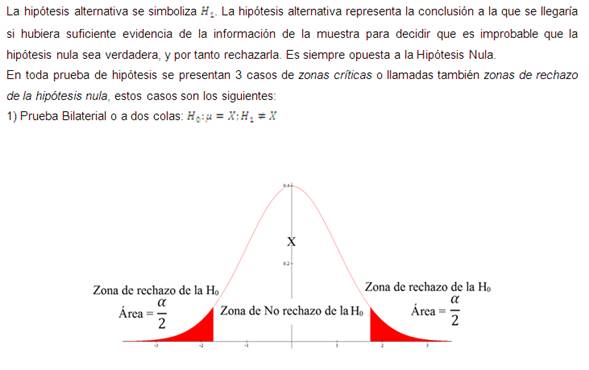
En toda prueba de hipótesis se pueden cometer 2 tipos de errores:
Conteste
1) ¿Qué es probar una hipótesis relativa a un parámetro?
2) ¿Cuándo se realiza una prueba de hipótesis?
3) ¿Qué es una hipótesis?
4) ¿Qué es prueba de hipótesis?
5) ¿Qué es hipótesis nula?
6) ¿Qué es hipótesis alternativa o alterna?
7) ¿Cuáles son los casos de zonas de rechazo de la hipótesis nula?
8) ¿Cuáles son los tipos de errores que se pueden cometer en toda prueba de hipótesis?
A) PRUEBA MEDIAS DE UNA MUESTRA
Se utiliza una prueba de una muestra para probar una afirmación con respecto a una media de una población única.
Si la población no es normal, o si se desconoce su forma, se emplea la ecuación anterior solamente para tamaños de muestra iguales o mayores 30, es decir, para n = 30
Nota: Se considera práctico utilizar la distribución t solamente cuando se requiera que el tamaño de la muestra sea menor de 30, ya que para muestras más grandes los valores t y z son aproximadamente iguales, y es posible emplear la distribución normal en lugar de la distribución t.
B) PRUEBA MEDIAS DE DOS MUESTRAS
Las pruebas de dos muestras se utilizan para decidir si las medias de dos poblaciones son iguales. Se requieren dos muestras independientes, una de cada una de las dos poblaciones. Considérese, por ejemplo, una compañía investigadora que experimentan con dos diferentes mezclas de pintura, para ver si se puede modificar el tiempo de secado de una pintura para uso doméstico. Cada mezcla es probada un determinado número de veces, y comparados posteriormente los tiempos medios de secado de las dos muestras. Una parece ser superior, ya que su tiempo medio de secado (muestra) es 30 minutos menor que el de la otra muestra.
Pero, ¿son realmente diferentes los tiempos medios de secado de las dos pinturas, o esta diferencia muestral es nada más la variación aleatoria que se espera, aun cuando las dos fórmulas presentan idénticos tiempos medios de secado? Una vez más, las diferencias casuales se deben distinguir de las diferencias reales.
Con frecuencia se utilizan pruebas de dos muestras para comparar dos métodos de enseñanza, dos marcas, dos ciudades, dos distritos escolares y otras cosas semejantes.
La hipótesis nula puede establecer que las dos poblaciones tienen medias iguales:
Cabe suponer que el valor real de Z, cuando es verdadera, está distribuido normalmente con una media de 0 y una desviación estándar de 1 (es decir, la distribución normal estandarizada) para casos en los que la suma n1 + n2 es igual o mayor de 30. Para tamaños más pequeños de muestra, Z estará distribuida normalmente sólo si las dos poblaciones que se muestrean también lo están.
Cuando no se conocen las desviaciones estándar de la población, y n1 + n2 es menor a 30, el valor estadístico de prueba es como el que se presenta a continuación.
4.2) ANÁLISIS DE VARIANZA
El análisis de varianza es una técnica que se puede utilizar para decidir si las medias de dos o más poblaciones son iguales. La prueba se basa en una muestra única, obtenida a partir de cada población. El análisis de varianza puede servir para determinar si las diferencias entre las medias muestrales revelan las verdaderas diferencias entre los valores medios de cada una de las poblaciones, o si las diferencias entre los valores medios de la muestra son más indicativas de una variabilidad de muestreo.
Si el valor estadístico de prueba (análisis de varianza) nos impulsa a aceptar la hipótesis nula, se concluiría que las diferencias observadas entre las medias de las muestras se deben a la variación casual en el muestreo (y por tanto, que los valores medios de población son iguales). Si se rechaza la hipótesis nula, se concluiría que las diferencias entre los valores medios de la muestra son demasiado grandes como para deberse únicamente a la casualidad (y por ello, no todas las medias de población son iguales).
Los datos para el análisis de varianza se obtienen tomando una muestra de cada población y calculando la media muestral y la variancia en el caso de cada muestra.
Existen tres supuestos básicos que se deben satisfacer antes de que se pueda utilizar el análisis de variancia.
Cabe observar que se debe utilizar n - 1, ya que se está trabajando con datos muestrales. De ahí que, para obtener la varianza muestral, el procedimiento sea el siguiente:
1) Calcular la media muestral
2) Restar la media de cada valor de la muestra.
3) Elevar al cuadrado cada una de las diferencias.
4) Sumar las diferencias elevadas al cuadrado.
5) Dividir entre n - 1
A) ESTIMACIÓN INTERNA DE VARIANZA
Una forma de calcular la varianza poblacional es sacar el promedio de las varianzas de las muestras. Es evidente que se podrá utilizar cualquiera de las varianzas muestrales, pero el promedio de todas ellas por lo general proporcionará la mejor estimación debido al mayor número de observaciones que representa. Como cada varianza muestral sólo refleja la variación dentro de una muestra en particular, la estimación de la varianza basada en el promedio de las varianzas muestrales se llama estimación interna de variancia. La estimación interna de variancia se calcula de la siguiente manera:
B) ESTIMACIÓN INTERMEDIANTE DE VARIANZA
Por tanto, no se puede utilizar por sí misma para determinar si las medias de la población podrían ser iguales. No obstante, sirve como una norma de comparación respecto a la cual puede evaluarse una segunda estimación llamada estimación intermediante de varianza. Esta segunda estimación es sensible a diferencias entre las medias de población.
La estimación interna de varianza sirve como una norma respecto a la cual se puede comparar la estimación intermediante de varianza.
La estimación de varianza entre muestras determina una estimación de las varianzas iguales de la población de una forma indirecta a través de una distribución de muestreo de medias.
Además, por el Teorema del Límite Central, se sabe que la distribución de muestreo de medias, obtenida de una población normal, estará distribuida normalmente, y que la desviación estándar de la distribución de muestreo (raíz cuadrada de su varianza) está directamente relacionada con el tamaño de la desviación estándar de la población (raíz cuadrada de la varianza de la población). Es decir,
