
RENTA TEMPORAL
El siguiente paso en la matemáticas financieras, es calcular el valor de una renta. Con objeto de su estudio, distinguiremos dos tres casos por orden de complejidad de sus cálculos, de más complejo a menos complejo:
El primer caso, el más genérico, corresponde, como ya hemos avanzado, a una renta de una duración determinada, en que las cantidades percibidas son distintas y sin relación entre ellas. Estas, nos permitirán explicar el concepto y posteriormente relacionarlas con los casos 2 y 3 que son casos específicos de este.
Antes de comenzar a analizar cada caso, si debemos precisar que, en estos casos, siempre utilizaremos el interés compuesto. También, debemos señalar que es especialmente importante para evitar errores, y antes de comenzar ningún cálculo, hacer la representación gráfica de los flujos, que consistirá en hacer una linea en la que indicaremos en que momento temporal se percibe cada cantidad. Esta herramienta nos permitirá asegurarnos cuantos periodos debemos descontar cada una de las cantidades.
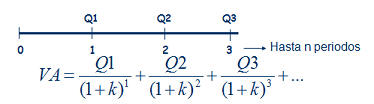 Siguiendo la imagen de la derecha, imaginemos una renta de las cantidades Q1, Q2, Q3,... que se cobran al final de cada periodo, 1, 2, 3,... El valor presente de esa renta temporal, consistirá simplemente en calcular el valor presente de cada una de las cantidades que componen la renta, tal y como representa la fórmula. Siguiendo la imagen de la derecha, imaginemos una renta de las cantidades Q1, Q2, Q3,... que se cobran al final de cada periodo, 1, 2, 3,... El valor presente de esa renta temporal, consistirá simplemente en calcular el valor presente de cada una de las cantidades que componen la renta, tal y como representa la fórmula.A partir de este sencillo ejemplo, podremos construir casos más complejos donde las cantidades tampoco sigan un patrón temporal, 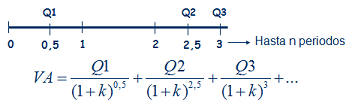 sino que se cobren en distintos momentos del tiempo, pero la base seguirá siendo la misma; el valor presente de las cantidades que componen la renta. Un ejemplo sería esta segunda imagen, donde los flujos no se producen al final de cada periodo, sino que se producen, Q1 a la mitad del primer periodo, Q2 entre el 2º y el 3º y Q3 al final del 3º. Además, se podría seguir complicando, considerando que el tipo de interés anual es distinto para cada cantidad, ya que no es lo mismo una operación aun año que a tres años (si por un depósito a 1 año pedimos un 5% anual, para un depósito a 3 años normalmente pediremos más de un 5% anual). sino que se cobren en distintos momentos del tiempo, pero la base seguirá siendo la misma; el valor presente de las cantidades que componen la renta. Un ejemplo sería esta segunda imagen, donde los flujos no se producen al final de cada periodo, sino que se producen, Q1 a la mitad del primer periodo, Q2 entre el 2º y el 3º y Q3 al final del 3º. Además, se podría seguir complicando, considerando que el tipo de interés anual es distinto para cada cantidad, ya que no es lo mismo una operación aun año que a tres años (si por un depósito a 1 año pedimos un 5% anual, para un depósito a 3 años normalmente pediremos más de un 5% anual).Como vemos, la parte más importante para el cálculo del valor de una renta, es comprender el momento temporal en que cada cantidad se produce, que es la base para conocer por cuanto tiempo deberemos retraerlo hasta el momento presente. Fórmula renta temporalTeniendo en cuenta el caso más genérico, podría expresarse como sigue: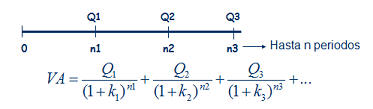 VA.- Valor actual o presente de la renta considerada Q1, Q2, Q3,... serían las cantidades que componen la renta n1, n2, n3,... serían el momento temporal en que se recibe cada cantidad de la renta k1, k2, k3,... serían los tipos de interés para cada periodo Además de los casos expuestos, donde hemos calculado el valor actual o presente, puede ser necesario el cálculo del valor futuro, como sería el caso del valor futuro de un plan de ahorro, por ejemplo, al que aportamos una cantidad mensual, trimestral o anual, que nos permitirá conocer que cantidad tendremos al final/vencimiento del producto. En este caso, en lugar de dividir cada flujo por el interés compuesto hasta el momento presente, únicamente deberemos multiplicar por ese interés compuesto hasta el momento futuro que deseemos.  RENTA INFINITA Este, es el último caso particular de rentas que analizaremos, y consiste en una renta que cobraremos por duración infinita (un buen ejemplo serían las pensiones de jubilación, pero también productos comercializados por las aseguradoras aunque menos conocidos). En este caso, también distinguiremos entre renta constante y creciente (por ejemplo rentas actualizadas con la inflación). 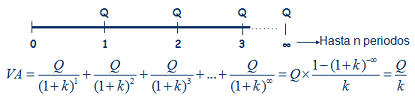 Para el caso de las rentas constantes nos encontraríamos en la figura de la derecha. Al ser infinitos periodos, y sustituyendo en la misma fórmula que utilizamos para las rentas temporales constantes, tendríamos que (1+k)∞ =0 lo que nos daría la expresión final. Para el caso de las rentas constantes nos encontraríamos en la figura de la derecha. Al ser infinitos periodos, y sustituyendo en la misma fórmula que utilizamos para las rentas temporales constantes, tendríamos que (1+k)∞ =0 lo que nos daría la expresión final.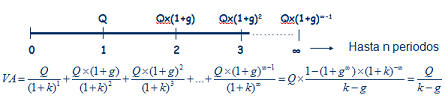 En el segundo caso, en el que las rentas crecen siguiendo una proporción g, sucedería algo similar, desapareciendo la mayor parte del numerador, tal y como se puede apreciar en la figura de la derecha. En el segundo caso, en el que las rentas crecen siguiendo una proporción g, sucedería algo similar, desapareciendo la mayor parte del numerador, tal y como se puede apreciar en la figura de la derecha.Por último, señalar también que, al igual que en las rentas temporales, no siempre las rentas se producen al final de cada periodo, sino que estas pueden producirse al principio de cada uno. En este caso, el valor actual/presente calculado con las fórmulas anteriores sería el valor calculado en el momento 1, no en el momento 0, por lo que únicamente deberíamos multiplicar el valor actual, así calculado, por (1+k) para anticipar un periodo toda la cantidad. |


 , la definición implica que en una distribución de probabilidad continua X se cumple P[X = a] = 0 para todo
, la definición implica que en una distribución de probabilidad continua X se cumple P[X = a] = 0 para todo 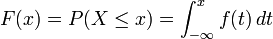

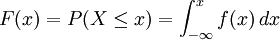
 una variable continua, una distribución de probabilidad o función de densidad de probabilidad (FDP) de
una variable continua, una distribución de probabilidad o función de densidad de probabilidad (FDP) de  tal que, para cualesquiera dos números
tal que, para cualesquiera dos números  y
y  siendo
siendo 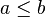 .
.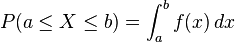
![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) es el área bajo la curva de la función de densidad; así, la función mide concentración de probabilidad alrededor de los valores de una variable aleatoria continua.
es el área bajo la curva de la función de densidad; así, la función mide concentración de probabilidad alrededor de los valores de una variable aleatoria continua. área bajo la curva de
área bajo la curva de 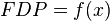 ) legítima, debe satisfacer las siguientes dos condiciones:
) legítima, debe satisfacer las siguientes dos condiciones: 0 para toda
0 para toda  .
.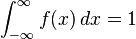
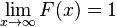 . Es decir, la probabilidad de todo el espacio muestral es 1.
. Es decir, la probabilidad de todo el espacio muestral es 1. . Es decir, la probabilidad del suceso nulo es cero.
. Es decir, la probabilidad del suceso nulo es cero. a
a 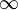 , como la de la
, como la de la 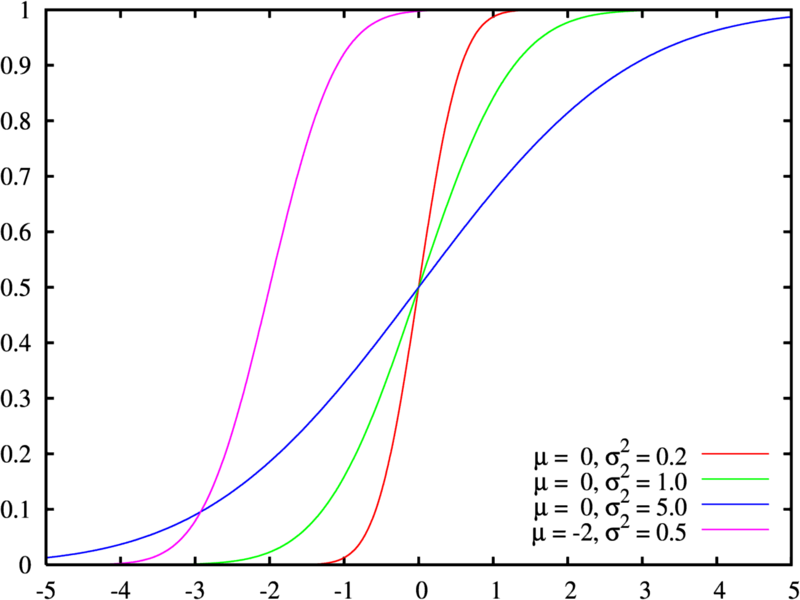

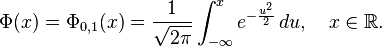
![\Phi(x)
=\frac{1}{2} \Bigl[ 1 + \operatorname{erf} \Bigl( \frac{x}{\sqrt{2}} \Bigr) \Bigr],
\quad x\in\mathbb{R},](http://upload.wikimedia.org/math/6/b/3/6b35a677ce8119b1eea63d02aaf3a9a3.png)
![\Phi_{\mu,\sigma^2}(x)
=\frac{1}{2} \Bigl[ 1 + \operatorname{erf} \Bigl( \frac{x-\mu}{\sigma\sqrt{2}} \Bigr) \Bigr],
\quad x\in\mathbb{R}.](http://upload.wikimedia.org/math/b/b/3/bb3ea66d01a7b6106216b79f48a859ba.png)
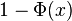 , se denota con frecuencia
, se denota con frecuencia  , y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.
, y es referida, a veces, como simplemente función Q, especialmente en textos de ingeniería.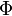 .
.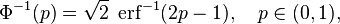
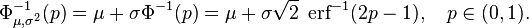
 es muy próxima a 1 y
es muy próxima a 1 y  está muy cerca de 0. Los límites elementales
está muy cerca de 0. Los límites elementales
 son útiles.
son útiles.
 y la
y la 
 proporciona el límite inferior.
proporciona el límite inferior.![M_X(t) = \mathrm{E} \left[ e^{tX} \right] = \int_{-\infty}^{\infty} \frac{1}{\sigma \sqrt{2\pi} } e^{-\frac{(x - \mu)^2}{2 \sigma^2}} e^{tx} \, dx = e^{\mu t + \frac{\sigma^2 t^2}{2}}](http://upload.wikimedia.org/math/0/8/3/0833056dec593a5766850cf55e4923dd.png)
![\begin{align}
\chi_X(t;\mu,\sigma) &{} = M_X(i t) = \mathrm{E}
\left[ e^{i t X} \right] \\
&{}=
\int_{-\infty}^{\infty}
\frac{1}{\sigma \sqrt{2\pi}}
e^{- \frac{(x - \mu)^2}{2\sigma^2}}
e^{i t x}
\, dx \\
&{}=
e^{i \mu t - \frac{\sigma^2 t^2}{2}}.
\end{align}](http://upload.wikimedia.org/math/2/6/6/266db4f786e5d21f0dee4788e41cb6fd.png)

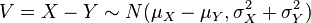 .
.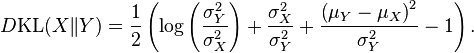

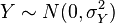
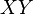

 donde
donde  es una
es una 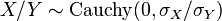 . De este modo la distribución de Cauchy es un tipo especial de
. De este modo la distribución de Cauchy es un tipo especial de 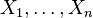 son variables normales estándar independientes, entonces
son variables normales estándar independientes, entonces 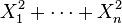 sigue una
sigue una  y la
y la 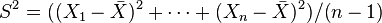 son independientes. Esta propiedad
son independientes. Esta propiedad  ~
~  , entonces
, entonces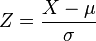
 ~
~  .
.
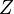 es una distribución normal estándar,
es una distribución normal estándar,  , entonces
, entonces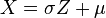
 y varianza
y varianza  .
.


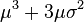
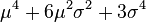
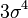

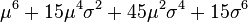
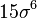



![E\left[X^{2k}\right]=\frac{(2k)!}{2^k k!} \sigma^{2k}.](http://upload.wikimedia.org/math/9/e/e/9ee2fb62550523bac223697b7ad104b0.png)