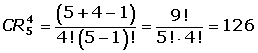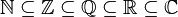TTEORÍA DE CONJUNTOS
La teoría de conjuntos es una rama de las matemáticas que estudia los conceptos de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.1
Sin embargo, la teoría de los conjuntos es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática.
Además, la propia teoría de conjuntos es objeto de estudio per se, no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables ocontradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.
TEORÍA BÁSICA DE CONJUNTOS
La teoría de conjuntos más elemental es una de las herramientas básicas del lenguaje matemático. Dados unos elementos, unos objetos matemáticos como números o polígonos por ejemplo, puede imaginarse una colección determinada de estos objetos, un conjunto. Cada uno de estos elementos pertenece al conjunto, y esta noción de pertenencia es la relación relativa a conjuntos más básica. Los propios conjuntos pueden imaginarse a su vez como elementos de otros conjuntos. La pertenencia de un elemento a a un conjunto A se indica como a ∈ A.
Una relación entre conjuntos derivada de la relación de pertenencia es la relación de inclusión. Una subcolección de elementos B de un conjunto dado A es un subconjunto de A, y se indica como B ⊆ A.
- Ejemplos.
- Los conjuntos numéricos usuales en matemáticas son: el conjunto de los números naturales N, el de los números enteros Z, el de los números racionales Q, el de los números reales R y el de los números complejos C. Cada uno es subconjunto del siguiente:
- El espacio tridimensional E3 es un conjunto de objetos elementales denominados puntos p, p ∈ E3. Las rectas r y planos α son conjuntos de puntos a su vez, y en particular son subconjuntos de E3, r ⊆ E3 y α ⊆ E3.
EJEMPLOS
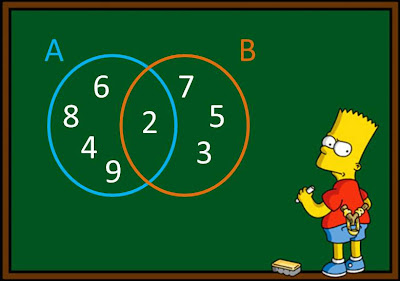
1.- Sean A ={1,2,3,4}; B ={2,4,6,8}; C ={3,4,5,6}
Hallar a).- A U B; b).- A U C; c).- B U C; d).- B U B
Solución:
A U B = {1,2,3,4,6,8}
A U C = {1,2,3,4,5,6}
B U C = {2,4,6,3,5}
B U B = {2,4,6,8
2.- Dado el conjunto A = {6,2,8,4,3} encontrar todos los subconjuntos de A que se puedan construir con sus elementos, es decir el conjunto potencia.
2A ={ {6},{2},{8},{4},{3},{6,2},{6,8},{6,4},{6,3},{2,8},{2,4},{2,3},{8,4},{8,3},{4,3},
{6,2,8},{6,2,4},{6,2,3},{6,8,4},{6,8,3},{6,4,3},{2,8,4},{2,8,3},{2,4,3},{8,4,3},{6,2,8,4},{6,2,8,3},
{2,8,4,3,},{6,8,4,3,},{6,2,4,3,},{6,2,8,4,3},{ }}
PRINCIPIO FUNDAMENTAL DE CONTEO
El principio básico o fundamental de conteo se puede utilizar para determinar los posibles resultados cuando hay dos o más características que pueden variar.
Ejemplo: El helado puede venir en un cono o una tasa y los sabores son chocolate, fresa y vainilla.
/ tasa de chocolate
/ chocolate <
/ \ cono de chocolate
/
/ / tasa de fresa
<-- fresa <
\ \ cono de fresa
\
\ / tasa de vainilla
\ vainilla <
\ cono de vainilla
El diagrama anterior se llama diagrama de árbol y muestra todas las posibilidades. El diagrama de árbol también se puede ordenar de otra forma. Ambos diagramas tienen un total de 6 resultados.
/ tasa de chocolate
/
/ tasa <-- tasa de fresa
/ \
/ \ tasa de vainilla
/
<
\
\ / cono de chocolate
\ /
\ cono <-- cono de fresa
\
\ cono de vainilla
Para determinar la cantidad total de resultados, multiplica la cantidad de posibilidades de la primera característica por la cantidad de posibilidades de la segunda característica. En el ejemplo anterior, multiplica 3 por 2 para obtener 6 posibles resultados.
Si hay más de dos resultados, continúa multiplicando las posibilidades para determinar el total de resultados.
PERMUTACIONES.
En matemáticas, una permutación es la variación del orden o de la disposición de los elementos de un conjunto.
Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".
La definición intuitiva de permutación, como ordenamientos o arreglos de los elementos de un conjunto se formaliza con el uso del lenguaje de funciones matemáticas.
|
Para ilustrar la definición, retomemos el ejemplo descrito en la introducción. En el ejemplo, X={1, 2, 3}.
Entonces, cada correspondencia uno a uno entre el conjunto {1, 2, 3} a sí mismo equivale a una forma de ordenar los elementos.
Por ejemplo, la asignación biyectiva dada por
- 1 → 1
- 2 → 2
- 3 → 3
puede hacerse corresponder al ordenamiento "1, 2, 3".
Por otro lado, la asignación biyectiva dada por
- 1 → 3
- 2 → 2
- 3 → 1
puede hacerse corresponder al ordenamiento "3, 2, 1".
En la definición de permutación, no se establece condición alguna sobre X, el cual puede incluso ser infinito. Sin embargo, es común considerar únicamente el caso en que X es un conjunto finito al estudiar permutaciones.
Dado un conjunto finito  de
de  elementos, el número de todas las permutaciones es igual a factorial de n:
elementos, el número de todas las permutaciones es igual a factorial de n:
 de
de  elementos, el número de todas las permutaciones es igual a factorial de n:
elementos, el número de todas las permutaciones es igual a factorial de n: .
.
Demostración: Dado que hay formas de escoger el primer elemento y, una vez escogido éste, sólo
tenemos  formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos
formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos ![[n-(k-1)]\,\!](http://upload.wikimedia.org/math/8/f/4/8f46046174b5f2caf438a978873d5f94.png) posibles elementos para escoger, lo que nos lleva a que tenemos
posibles elementos para escoger, lo que nos lleva a que tenemos 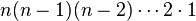 formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.
formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.
 formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos
formas de escoger el segundo elemento, y así sucesivamente, vemos que cuando llegamos al elemento k-ésimo sólo tenemos ![[n-(k-1)]\,\!](http://upload.wikimedia.org/math/8/f/4/8f46046174b5f2caf438a978873d5f94.png) posibles elementos para escoger, lo que nos lleva a que tenemos
posibles elementos para escoger, lo que nos lleva a que tenemos 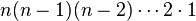 formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.
formas de ordenar el conjunto, justamente lo que enunciamos anteriormente.
Ejemplo: sea el conjunto A={1,2,3} en este caso hay 6 permutaciones, en forma compacta: 123, 132, 213, 231, 312, 321. En álgebra, para estudiar los grupos simétricos se presentan entre paréntesis y en dos filas, en la primera siempre aparece 1 2 3.
Una variante de lo mismo, si se va a formar un comité que involucra presidente, tesorero y secretario, habiendo tres candidatos a, b, c ; cuando se elige por sorteo los cargos sucesivamente, hay seis posibilidades u ordenaciones: abc, acb, bca, bac, cab, cba.
ejemplos:
¿Cuántos números de 5 cifras diferentes se puede formar con los dígitos: 1, 2, 3, 4, 5.?
m = 5 n = 5
Sí entran todos los elementos. De 5 dígitos entran sólo 3.
Sí importa el orden. Son números distintos el 123, 231, 321.
No se repiten los elementos. El enunciado nos pide que las cifras sean diferentes.
¿De cuántas formas distintas pueden sentarse ocho personas en una fila de butacas?
Sí entran todos los elementos. Tienen que sentarse las 8 personas.
Sí importa el orden.
No se repiten los elementos. Una persona no se puede repetir.
¿De cuántas formas distintas pueden sentarse ocho personas alrededor de una mesa redonda?
Con las cifras 2, 2, 2, 3, 3, 3, 3, 4, 4; ¿cuántos números de nueve cifras se pueden formar?
m = 9 a = 3 b = 4 c = 2 a + b + c = 9
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.
Con las letras de la palabra libro, ¿cuántas ordenaciones distintas se pueden hacer que empiecen por vocal?
La palabra empieza por i u o seguida de las 4 letras restantes tomadas de 4 en 4.
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.

¿Cuántos números de cinco cifras distintas se pueden formar con las cifras impares? ¿Cuántos de ellos son mayores de 70.000?
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.

Si es impar sólo puede empezar por 7 u 8

COMBINACIONES.

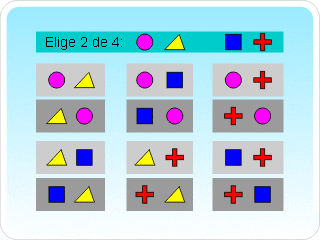
Una combinación es un arreglo donde el orden NO es importante. La notación para las combinaciones es C(n,r) que es la cantidad de combinaciones de “n” elementos seleccionados, “r” a la vez. Es igual a la cantidad de permutaciones de “n” elementos tomados “r” a la vez dividido por “r” factorial. Esto sería P(n,r)/r! en notación matemática.
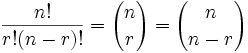
Ejemplo:
Si se seleccionan cinco cartas de un grupo de nueve, ¿cuantas combinaciones de cinco cartas habría?
La cantidad de combinaciones posibles sería:
P(9,5)/5! = (9*8*7*6*5)/(5*4*3*2*1) = 126 combinaciones posibles.
Calcular el número de combinaciones de 10 elementos tomados de 4 en 4.
- En una clase de 35 alumnos se quiere elegir un comité formado por tres alumnos. ¿Cuántos comités diferentes se pueden formar?
- No entran todos los elementos.
- No importa el orden: Juan, Ana.
- No se repiten los elementos.

No entran todos los elementos. Sólo elije 4..
No importa el orden. Da igual que elija 2 botellas de anís y 2 de ron, que 2 de ron y 2 de anís.
Sí se repiten los elementos. Puede elegir más de una botella del mismo tipo.